Lecture 8

Composition space and mineral stability

Compositions space

We have already discussed different ways of writing mineral formulas. There are often times that we want to express these formulas graphically. We call this graphic depiction the mineral’s composition space, the minimum number of chemical species necessary to describe the composition of mineral phases being considered. We will see how to use this approach to (1) plot specific mineral compositions, (2) show, graphically, the extent of solid solution, and (3) depict chemical reactions among different mineral phases. In doing this we will be plotting in two dimensions (because it’s easiest) … to show more than two different chemical species, we’ll introduce plotting on ternary diagrams (something that petrologists like to do!).

Two-component systems

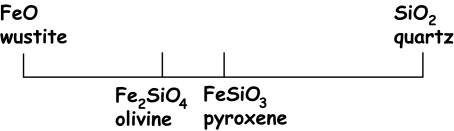
The diagram above shows the composition space defined by the two-component chemical system FeO – SiO₂. Note that the components can be oxide complexes rather than simple ions. In this simple example, the composition space is a straight line. Points on the line are defined by the iron end members of olivine and pyroxene. Note that these are shown as molar proportions rather than weight percent (although this would also be possible). For example, in this scheme, we plot FeSiO₃ as

1 FeO + 1 SiO₂ … in a similar vein, how do you decide the plotting positions for Fe₂SiO₄?

We can also use this strategy to show a solid solution series, and the location of a specific composition within that series:

Here the olivine end members forsterite and fayalite mark the ends of the line. How would you plot (Mg._1.5Fe_.5)SiO₄?

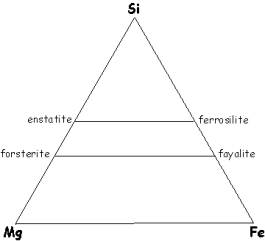
Three component systems are traditionally plotted on a ternary diagram, that is, on a planar triangle. Let’s look at the Si-Fe-Mg ternary (we’ve already looked at two parts of it):

Here we show the FeO-SiO₂ binary on one side of the triangle, and an analogous MgO-SiO₂ binary on the other side of the triangle. The solid solution series between the olivine and pyroxene end members form horizontal lines parallel to the base of the triangle.

Now let’s look at another ternary plot, that showing the pyroxenes and pyroxenoids:

In this example, there is one solid solution across the base of the triangle (the orthopyroxenes) and another solid solution across the middle of the triangle (the clinopyroxenes). At the apex of the triangle is wollastonite, which is not a true pyroxene but instead is what we call a pyroxenoid.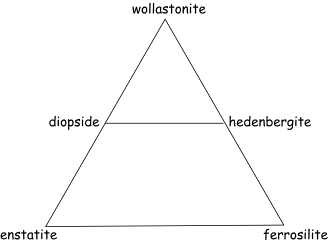 [NOTE: the 2 Ca in the structure can’t fit into the cation site normally occupied by the smaller Mg²⁺ or Fe²⁺, and thus changes the structure].

Let’s return to the binary example:

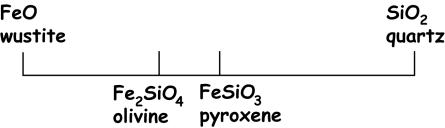
This diagram shows us more than simply the molar formula of each mineral constituent. It also illustrates the chemical reactions that can occur between different mineral phases. For example, note that pyroxene lies between olivine and quartz. Another way of stating this is to say that pyroxene can be made from combinations of olivine and quartz. This can be written as a chemical reaction:

This reaction can go in either direction… most common in the systems that we will be working with will be the spontaneous formation of pyroxene by reaction of olivine with SiO₂ in the melt (this reaction is common in basaltic systems).

This leads to the next point: the minerals that we find together in a given rock are a function of (1) which mineral or combination of minerals is stable, and (2) the bulk composition of the rock. The effect of bulk composition may be thought of as follows. If the bulk composition of a melt lay between olivine and pyroxene, then a rock formed from that melt could contain either olivine + pyroxene or olivine + quartz. It could not be composed solely of pyroxene or solely of olivine.

Let’s look at one more example:

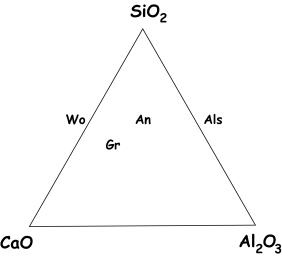This is a ternary diagram where the chemical components are SiO₂, CaO, and Al₂O₃. This ternary is important for the study of many metamorphic rocks. On the ternary are two minerals that you’ve already seen – quartz, which sits at the SiO₂ apex, and wollastonite (Wo), the calcic pyroxenoid. Also shown are the aluminosilicates (Als; sillimanite, kyanite, andalusite), the Ca-plagioclase feldspar anorthite (An) and the Ca-garnet grossular (Gr).

Why do they plot in these positions? Examine the following Table, which gives the composition of two of the minerals as (1) molar proportions and (2) molar % (determined by adding up the number of moles and normalizing to 100%).

Mineral	Moles CaO	Moles Al2O3	Moles SiO2	% CaO	% Al2O3	%SiO2
anorthite	1	1	2	25	25	50
grossular	3	1	3	43	14	43
wollastonite	1		1
kyanite		1	1

Fill out the rest of the Table for yourself…